TURUNAN FUNGSI
Turunan Fungsi
Turunan adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi
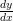 atau
atau 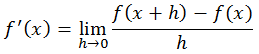
Rumus
Dasar Turunan dari Turunan Fungsi
Aturan-aturan dalam turunan fungsi
ialah:
- f(x), menjadi f'(x) = 0
- Apabila f(x) = x, maka f’(x) = 1
- Aturan pangkat : apabila f(x) = xn, maka f’(x) = n X n – 1
- Aturan kelipatan konstanta : apabila (kf) (x) = k. f’(x)
- Aturan rantai : apabila ( f o g ) (x) = f’ (g (x)). g’(x))
Rumus-rumus turunan fungsi :
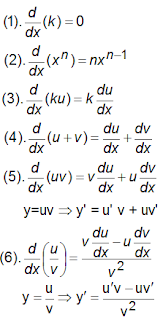
Rumus-Rumus
Turunan Fungsi Al Jabar
1.
Rumus
Turunan Fungsi Pangkat
Turunan Fungsi berbentuk pangkat,
turunannya dapat menggunakan rumus
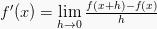 sebagai
berikut:
sebagai
berikut: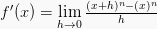
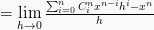
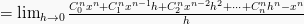
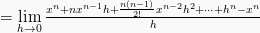

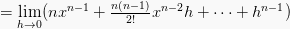
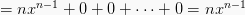
Maka, rumus turunan fungsi pangkat ialah:
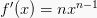
2. Rumus
turunan hasil kali fungsi
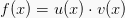
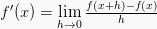
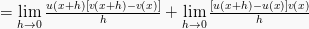
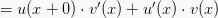
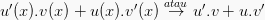
Maka, rumus turunan fungsinya ialah:
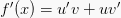
Rumus turunan fungsi pembagian dapat di tentukan dengan :
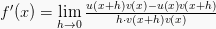
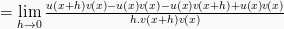
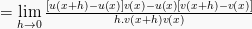
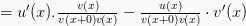
Maka, rumus turunan fungsinya adalah
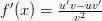
4.
Rumus turunan pangkat dari fungsi
Perlu diingat, apabila
maka 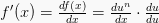 Atau,
Atau, 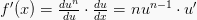 Maka, rumus turunan fungsinya
Maka, rumus turunan fungsinya
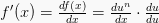 Atau,
Atau, 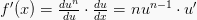 Maka, rumus turunan fungsinya
Maka, rumus turunan fungsinya
ialah: 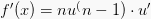
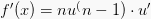
Rumus-rumus Turunan Trigonometri
Berdasarkan definisi turunan, maka dapat diperoleh rumus-rumus turunan
trigonometri yakni sebagai berikut:
(dengan u dan v masing-masing fungsi dari x), yakni:
1. 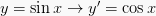
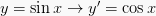
2. 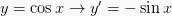
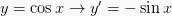
3. 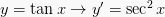
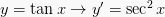
4. 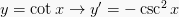
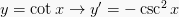
5. 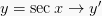
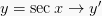
6. 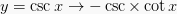
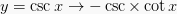
7. 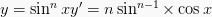
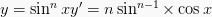
8. 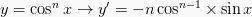
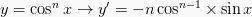
9. 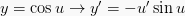
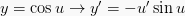
10. 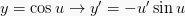
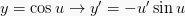
11. 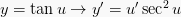
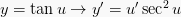
12. 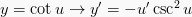
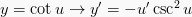
13. 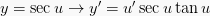
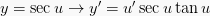
14. 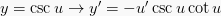
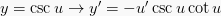
15. 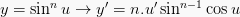
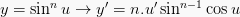
16. 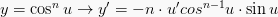
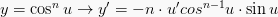














Komentar
Posting Komentar