BASIS RUANG DENGAN BARIS, BASIS RUANG DENGAN KOLOM, RANK, NULITAS
- DIMENSI
Definisi:
Suatu ruang vektor tak nol V disebut berdimensi terhingga jika V berisi suatu himpunan vektor terhingga {v1,v2,…vn} yang membentuk suatu basis. Jika tak ada himpunan yang seperti itu, maka V disebut berdimensi tak hingga. Ruang vektor nol berdimensi terhingga
TEOREMA:
jika V adalah adalah suatu ruang vektor berdimensi terhingga dan {v1,v2,…vn} adalah sembarang basis, maka:
- Setiap himpunan dengan lebih dari n vektor adalah tak bebas secara linear
- Tidak ada himpunan dengan vektor yang kurang dari n yang merentang V.
TEOREMA:
- Semua basis untuk suatu ruang vektor berdimensi terhingga mempunyai jumlah vektor yang sama
- Suatu ruang vektor berdimensi terhingga V, yang dinyatakan dengan dim(V), didefinisikan sebagai jumlah vektor dalam suatu basis untuk V. Ruang vektor nol mempunyai dimensi nol.
Contoh
Menentukan basis dan dimensi ruang solusi dari SPL homogen
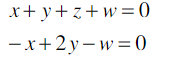
penyelesaian
Kita dapat menyatakan sistem ini dalam bentuk sebagai berikut
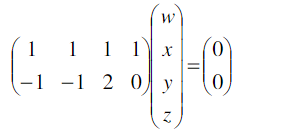
⇒ 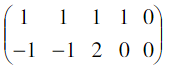
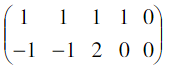
⇒ 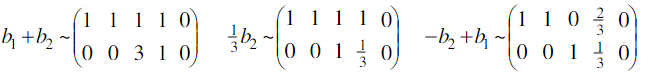
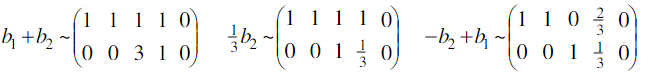
jadinya
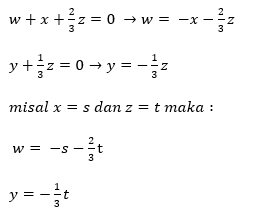
membentuk ruang solusi SPL yaitu
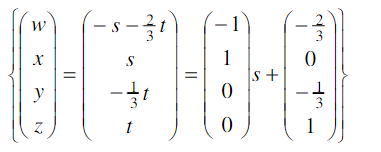
yang menunjukkan bahwa vektor vektor 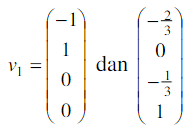 merentang ruang solusi tersebut. Karena v1 dan v2 tidak saling berkelipatan satusama lain maka kedua vektor ini saling bebas bebas linear.Jadi (v1,v2) adalah basis bagi ruang solusi SPL yang dimaksud yang berdimensi 2.
merentang ruang solusi tersebut. Karena v1 dan v2 tidak saling berkelipatan satusama lain maka kedua vektor ini saling bebas bebas linear.Jadi (v1,v2) adalah basis bagi ruang solusi SPL yang dimaksud yang berdimensi 2.
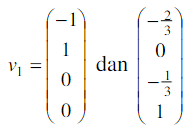 merentang ruang solusi tersebut. Karena v1 dan v2 tidak saling berkelipatan satusama lain maka kedua vektor ini saling bebas bebas linear.Jadi (v1,v2) adalah basis bagi ruang solusi SPL yang dimaksud yang berdimensi 2.
merentang ruang solusi tersebut. Karena v1 dan v2 tidak saling berkelipatan satusama lain maka kedua vektor ini saling bebas bebas linear.Jadi (v1,v2) adalah basis bagi ruang solusi SPL yang dimaksud yang berdimensi 2.
RUANG BARIS DAN RUANG KOLOM
- Jika A adalah matriks mxn maka subruang
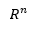 yang direntang oleh vektor-vektor baris dari A disebut ruang baris dari A. Subruang dari
yang direntang oleh vektor-vektor baris dari A disebut ruang baris dari A. Subruang dari 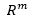 yang direntang oleh vektor-vektor kolom dari A disebut ruang kolom dari A.
yang direntang oleh vektor-vektor kolom dari A disebut ruang kolom dari A.
TEOREMA
- Jika suatu matriks U berada dalam bentuk baris eselon maka vektor-vektor baris dengan utama 1 (yaitu vektor-vektor tak-nol) membentuk suatu basis untuk ruang baris U dan vektor-vektor kolom dengan utama 1 dari vektor-vektor baris membentuk suatu basis untuk ruang kolom dari U.
misalkan matriks :
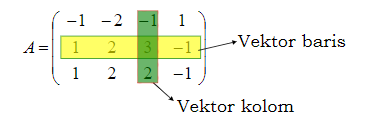
dengan melakukan OBE diperoleh
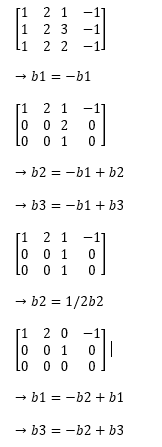
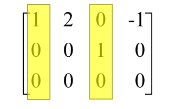 → perhatikan kolom-kolom pada matriks hasil OBE
→ perhatikan kolom-kolom pada matriks hasil OBE
matriks A mempunyai basis ruang kolom yaitu :
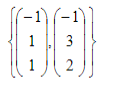
basis ruang baris diperoleh dengan cara,Mentransposkan terlebih dahulu matriks A, lakukan OBE pada 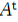 ,sehingga diperoleh :
,sehingga diperoleh :
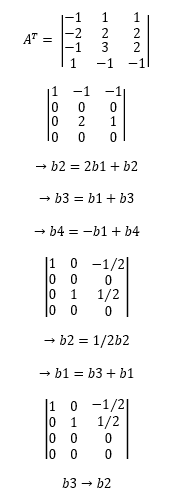 ⇒
⇒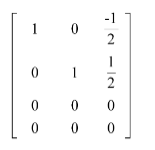
Kolom-kolom pada matriks hasil OBE yang memiliki satu utama berseseuaian dengan matriks asal (A). Ini berarti, matriks A tersebut mempunyai basis ruang baris :
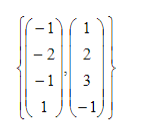
Defnisi RANK dan NULITAS
Dimensi dari ruang baris dan ruang kolom dari suatu matriks A disebut rank dari A dan dinyatakan sebagai rank(A). Dimensi dari ruang nul dari A disebut sebagai nulitas dari A
dan dinyatakan sebagai nulitas(A).
Tentukan rank dan nulitas dari matriks berikut ini:
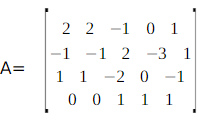
Penyelesaian:
dengan melakukan OBE diperoleh

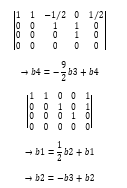 ⇒
⇒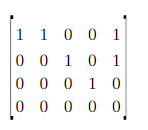
karena terdapat 3 baris tak nol (atau secara ekuivalen, 3 satu utama),ruang baris dan ruang kolom keduanya berdimensi 3 sehingga rank dari (A)=3. Untuk menentukan nutulitas dari A,maka kita harus menentukan dimensi dari ruang solusi linier Ax=0. Sistem persamaan yang bersesuaian adalah
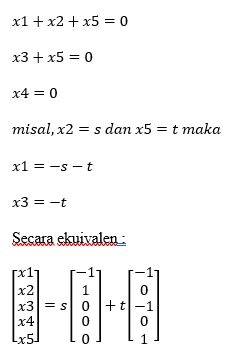
Kedua vektor tersebut membentuk basis untuk ruang solusi, sehingga nulitas(A) = 4.

izin bertanya kenapa nulitasnya 4 bkannya 2 ya kak?
BalasHapusUdh nyontek msih protes
HapusLahhh ditanya kagak dijawab🤣🤣
Hapusiya nullitasnya 2
BalasHapusMakasih kak
BalasHapus