SIFAT HARGA MUTLAK.
Harga mutlak disimbolkan dengan garis vertikal sebagai tanda kurungnya. Misalnya nilai mutlak dari  dituliskan
dituliskan  . Harga Mutlak didefinisikan sebagai sebuah notasi yang menyatakan nilai yang selalu positif. Suatu fungsi yang berada dalam kurung harga mutlak selalu bernilai positif dan tidak mungkin negative.
. Harga Mutlak didefinisikan sebagai sebuah notasi yang menyatakan nilai yang selalu positif. Suatu fungsi yang berada dalam kurung harga mutlak selalu bernilai positif dan tidak mungkin negative.

───┼─────┼─────┼─> R
-x 0 x
• Secara Geometri:
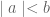 jika dan hanya jika
jika dan hanya jika  dimana
dimana 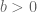
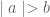 jika dan hanya jika
jika dan hanya jika  atau
atau 



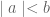 jika dan hanya jika
jika dan hanya jika  dimana
dimana 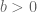
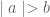 jika dan hanya jika
jika dan hanya jika  atau
atau 

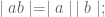
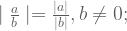
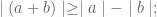
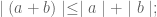


Contoh Soal (1)
Selesaikanlah persamaan -3|x-4|+5 = 14
Jawab :
Contoh Soal (2)
 Penyelesaiannya ;
Penyelesaiannya ;

•Definisi nilai mutlak :

───┼─────┼─────┼─> R
-x 0 x
• Secara Geometri:
|x| menyatakan jarak dari x
ke titik asal.
|x
– y| = jarak diantara x
dan y
• |x|≥
0 untuk
setiap bilangan real x dan
|x|
= 0 jika
dan hanya
jika x = 0.
A. Pengertian Nilai Mutlak, yaitu :
V
B. Beberapa sifat-sifat nilai mutlak adalah sebagai berikut ini :
Jika 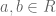 , maka :
, maka :
|x|2
= x2
|x|
< |y| jika
dan hanya jika x2
< y2
Sifat-sifat tersebut disarankan untuk dihafal. Yang sering menipu adalah untuk sifat  .
.
Ini banyak digunakan untuk beberapa persamaan yang mengikutkan suatu variabel. Ingat betul untuk sifat yang satu ini.
Persamaan Nilai Mutlak
- Nilai mutlak dari sebuah bilangan dapat didefinisikan sebagai jarak bilangan
tersebut terhadap titik 0 pada garis bilangan tanpa memperhatikan arahnya. Dari
pengertian tersebut dapat kita ambil contoh |x| = 4 memiliki dua buah
penyelesaian dikarenakan ada dua buah bilangan yang jaraknya 4 titik dari 0
yaitu x = 4 dan x = -4 seperti bisa kalian lihat
pada gambar di bawah ini:
Konsep tersebut dapat kita perluas penggunaannya untuk menyelesaikan
persoalan-persoalan yang berkaitan dengan bentuk aljabar yang terletak pada
simbol-simbol nilai mutlak. Hal tersebut dijelaskan oleh sifat persamaan nilai mutlak berikut ini:
“Apabila x adalah sebuah bentuk aljabar, sedangkan n merupakan bilangan real positif, maka |x| = n dapat diimplikasikan menjadi x = n atau x = -n”
Cara Menyelesaikan Persamaan
Nilai Mutlak
Contoh Soal (1)
Selesaikanlah persamaan -3|x-4|+5 = 14
Jawab :
-3|x-4|+5 = 14
-3|x-4|= 14 - 5
-3|x-4|= 9
|x-4|= -3
Contoh Soal (2)
 Penyelesaiannya ;
Penyelesaiannya ;


Komentar
Posting Komentar