MACAM - MACAM BILANGAN.

Pengertian Bilangan

Bilangan adalah suatu konsep matematika yang digunakan sebagai pencacahan dan pengukuran. Lambang atau simbol untuk mewakili bilangan disebut dengan angka atau lambang bilangan.

Bilangan adalah suatu konsep matematika yang digunakan untuk pencacahan dan pengukuran atau lebih mudahnya bilangan adalah suatu sebutan untuk menyatakan jumlah/banyaknya sesuatu. Simbol ataupun lambang yang digunakan untuk mewakili suatu bilangan disebut sebagai angka atau lambang bilangan. Dalam matematika, konsep bilangan selama bertahun-tahun lamanya telah diperluas untuk meliputi bilangan nol, bilangan negatif, bilangan rasional, bilangan irasional, dan bilangan kompleks.

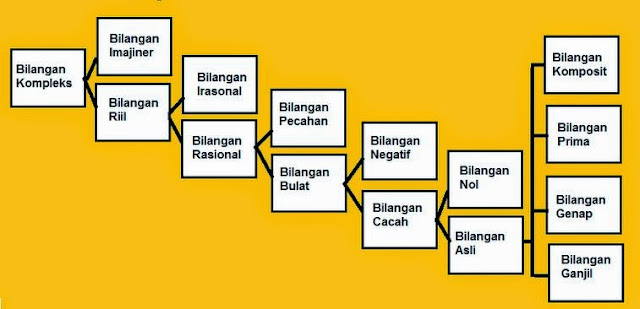
Macam-macam bilangan :

• Bilangan Bulat
• Bilangan Genap
• Bilangan Ganjil
• Bilangan Cacah
• Bilangan Asli
• Bilangan Prima
• Bilangan Pecahan
• Bilangan Rasional
• Bilangan Irrasional
• Bilangan Komposit
• Bilangan Riil
• Bilangan Kuadrat
• Bilangan Kubik
• Bilangan Romawi

1. Bilangan Bulat
• Bilangan Bulat adalah semua bilangan selain pecahan atau desimal, terdiri dari bilangan bulat positip, nol dan bilangan bulat negatif.
• Contah:  dst.... -3,-2,-1,0,1,2,3...dst
2. Bilangan Genap
• Bilangan Genap adalah bilangan bulat yang habis dibagi dua.
• Contoh: 2,4,6,8,10,12,14......dst
3. Bilangan Ganjil
• Bilangan Ganjil adalah bilangan bulat yang tidak habis dibagi dua.
• Contoh: 1,3,5,7,9,11,13,15.....dst
4. Bilangan Cacah
• Bilangan Cacah adalah bilangan bulat positif yang dimulai dari angkal nol (0) sampai dengan tak terhingga.
• Contoh: 0,1,3,4,5,6,7,8,9,10,11.... dst
5. Bilangan Asli
• Bilangan Asli adalah bilangan bulat positif yang dimualai dengan angka satu (1) sampai tak terhingga.
• Contoh: 1,2,3,4,5,67,8,9,10,11,... dst
6. Bilangan Prima
• Bilangan Prima adalah bilangan yang hanya dapat dibagi oleh angka 1 atau bilangan itu sendiri.
• Contoh: 2,3,5,7,... dst
7. Bilangan Pecahan
• Bilangan pecahan adalah bilangan yang terdiri dari pembilang dan penyebut.
• Contoh : 5/7
• 5 dinyatakan sebagai bilangan pembilang
• 7 dinyatakan sebagai bilangan penyebut
8. Bilangan Rasional
• Bilangan Rasional adalah bilangan yang dapat dinyatakan sebagai a/b dimana a dan b adalah bilangan bulat dan b tidak sama dengan 0.
• Contoh: 2/1 , 1/2, 2/3, 3/4, .... dst
9. Bilangan Irrasional
• Bilangan Irrasional adalah bilangan riil yang tidak bisa dibagi (hasil baginya tidak pernah berhenti) atau bilangan yang tidak bisa dibuat pecahannya.
• Contoh: I = { √2, √3, √5, √6, √7, ..... }
  Keterangan tambahan: √4 = 2, berarti √4 bukan termasuk bilangan irrasional.
10. Bilangan Riil 
• Bilangan Riil adalah semua bilangan rasional dan irrasional. 
• Contoh: 1,3,5,3,6, 1/2, 3/4,...dst
11. Bilangan Komposit
• Bilangan Komposit adalah bilangan asli lebih besar dari 1 yang bukan merupakan bilangan prima.
• Contohnya: K = {4, 6, 8, 9, 10, 12, ….}

12.   Bilangan Kuadrat

• Bilangan kuadrat adalah bilangan yang dihasilkan dari perkalian suatu bilangan dengan bilangan itu sendiri sebanyak dua kali dan disimbolkan dengan pangkat 2
• Contoh: D = { 22, 32, 42, 52, ..... }

  13.   Bilangan Kubik

• Bilangan Kubik adalah perkalian bilangan dengan bilangan itu sendiri sebanyak tiga kali
• Contoh: 

  	23	=	8
  	33	=	27
  	43	=	64
  	103	=	1.000
  	203	=	8.000
  	303	=	27.000
  	403	=	64.000

 14.   Bilangan Romawi

• Bilangan Romawi adalah sistem penomoran yang berasal dari Romawi kuno. Sistem penomoran ini memakai huruf Latin untuk melambangkan angka numerik.
• Contoh:  

  Simbol	Hasil
  I	1 (satu) (unus)
  V	5 (lima) (quinque)
  X	10 (sepuluh) (decem)
  L	50 (lima puluh) (quinquaginta)
  C	100 (seratus) (centum)
  D	500 (lima ratus) (quingenti)
  M	1.000 (seribu) (mille)

                 

Simbol	Hasil
V	5.000 (lima ribu)
X	10.000 (sepuluh ribu)
L	50.000 (lima puluh ribu)
C	100.000 (seratus ribu)
D	500.000 (lima ratus ribu)
M	1.000.000 (satu juta)

Romawi	Alternatif	Arab	Catatan
tidak ada	tidak ada	0	Tidak diperlukan.
I	Ⅰ	1
II	ⅠⅠ (atau Ⅱ)	2
III	ⅠⅠⅠ (atau Ⅲ)	3
IV	ⅠⅤ (atau Ⅳ)	4	IIII Masih Digunakan Untuk Jam
V	Ⅴ	5
VI	ⅤⅠ (atau Ⅵ)	6
VII	ⅤⅠⅠ (atau Ⅶ)	7
VIII	ⅤⅠⅠⅠ (atau Ⅷ)	8
IX	ⅠⅩ (atau Ⅸ)	9
X	Ⅹ	10
XI	ⅩⅠ (atau Ⅺ)	11
XII	ⅩⅠⅠ (atau Ⅻ)	12
XIII	ⅩⅠⅠⅠ	13
XIV	ⅩⅠⅤ	14
XV	ⅩⅤ	15
XIX	ⅩⅠⅩ	19
XX	ⅩⅩ	20
XXX	ⅩⅩⅩ	30
XL	ⅩⅬ	40
L	Ⅼ	50
LX	ⅬⅩ	60
LXX	ⅬⅩⅩ	70
LXXX	ⅬⅩⅩⅩ	80
XC	ⅩⅭ	90
C	Ⅽ	100
CC	ⅭⅭ	200
CD	ⅭⅮ	400
D	Ⅾ	500
DCLXVI	ⅮⅭⅬⅩⅤⅠ	666	Menggunakan setiap simbol utama.
CM	ⅭⅯ	900
M	Ⅿ	1000
MCMXLV	ⅯⅭⅯⅩⅬⅤ	1945
MCMXCIX	ⅯⅭⅯⅩⅭⅠⅩ	1999
MM	ⅯⅯ	2000
MMM	ⅯⅯⅯ	3000
MMMM	ⅯⅯⅯⅯ	4000
IƆƆ	ⅠƆƆ	5000	I diikuti dengan dua buah C terbalik.

15.  Pengertian bilangan nol

Bilangan nol adalah bilangan nol itu sendiri (0)

Contoh: N = { 0 }

16.  Pengertian bilangan Real

Bilangan real adalah bilangan yang merupakan gabungan dari bilangan rasional dan bilangan irrasional itu sendiri.
Contoh: R = { 0, 1, ¼, ⅔, √2, √5, ..... }

17. Pengertian bilangan negatif

Bilangan negatif adalah bilangan bernilai negatif.
Contoh: N = { -3, -5, ¼, .... }
Keterangn tambahan: -2/-3 = ⅔, berarti -2/-3 bukan termasuk bilangan negatif.

18. Pengertian bilangan positif

Bilangan positif adalah bilangan yang bernilai positif selain nol.
Contoh: P = { 2, 3, 4, ¼, .... }

19. Pengertian bilangan Kompleks

Bilangan kompleks adalah bilangan yang angota-anggotanya (a + bi) dimana a, b ϵ R, i2 = -1. Dengan a bagian bilangan rill dan b bagian dari bilangan imajiner.
Contoh: K = { 2-3i, 8+2, .... }

20. Pengertian bilangan imajiner

Bilangan imajiner adalah bolangan i (satuan imajiner) dimana i adalah lambang bilangan baru yang bersifat i2 = -1.
Contoh: M = { i, 4i, 5i, ..... }