SISTEM PERSAMAAN LINIER ( SPL ) METODE GAUS,GAUS JORDAN,CRAMER

-
Eliminasi Gauss
Metode eliminasi gauss termasuk dalam metode penyelesaian persamaan linear dengan cara langsung. Inti dari metode ini adalah membawa persamaan kedalam bentuk matriks dan menyederhanakan matriks menjadi bentuk segitiga atas. Setelah mendapat bentuk matriks tersebut dilakukan subtitusi balik untuk mendapat nilai dari akar persamaan tadi. Untuk lebih jelasnya kita perhatikan contoh berikut.
Contoh eliminasi Gauss dan eliminasi Gauss-Jordan
Selesaikan bentuk SPL berikut:
2x1 + x2 + 4x3 = 16
3x1 + 2x2 + x3 = 10
x1 + 3x2 + 3x3 = 16
dalam bentuk matriks:

Penyelesaian (Eliminasi Gauss):
Langkah (1)

Langkah (2)
Langkah (3)
Langkah (4)


Langkah (5)

Langkah (6)

 langkah (7)
Dengan demikian diperoleh:
Untuk memperoleh x1 dan x2 subt pers (3) ke pers. (1) dan (2), x3 = 3
x2 – 10(3) = -28
x2 – 30 = -28
x2 = 2
Untuk memperoleh x1:


Jadi diperoleh x1 = 1, x2 = 2 dan x3 = 3
Kelebihan Eliminasi Gauss
  • menentukan apakah sistem konsisten
  • menghilangkan kebutuhan untuk menulis ulang variabel setiap langka
  • lebih mudah untuk memecahkan
  • tidak ada error
Kekurangan Eliminasi Gauss
  • memiliki masalah akurasi saat pembulatan desimal
Eliminasi Gauss Jordan
Metode ini pengembangan dari metode eliminasi gauss. Dimana tujuan kita membuat matriks identitas bukan lagi segitiga atas sehingga tidak diperlukan lagi subtitusi balik untuk mencari nilai dari akar persamaan. Contoh penyelesaian Eliminasi Gauss Jordan dibawah ini berhubungan dengan contoh penyelesaian eliminasi gauss diatas tadi dimana langkah(1) – langkah(3) sama sedangkan untuk langkah selanjutnya seperti ini:



dari matriks diatas langsung dapat diketahui nilai dari x1 x2 x3 tanpa subtitusi balik
Kelebihan Eliminasi Gauss Jordan
  • Mengubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.
  • Merupakan variasi dari eliminasi gauss dengan kebutuhan dapat mgenyelesaikan matriks invers
Kekuragan Eliminasi Gauss Jordan
  • Terdapat error

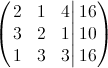
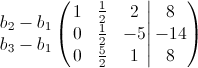
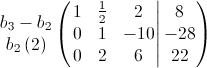
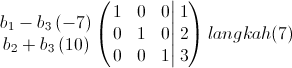
Komentar

Posting Komentar

Postingan populer dari blog ini

BASIS RUANG DENGAN BARIS, BASIS RUANG DENGAN KOLOM, RANK, NULITAS

-
Gambar
DIMENSI  Definisi: Suatu ruang vektor tak nol V disebut berdimensi terhingga jika V berisi suatu himpunan vektor terhingga { v 1, v 2,… v n} yang membentuk suatu basis. Jika tak ada himpunan yang seperti itu, maka V disebut berdimensi tak hingga. Ruang vektor nol berdimensi terhingga TEOREMA: jika V adalah adalah suatu ruang vektor berdimensi terhingga dan { v 1, v 2,… v n} adalah sembarang basis, maka: Setiap himpunan dengan lebih dari n vektor adalah tak bebas secara linear Tidak ada himpunan dengan vektor yang kurang dari n yang merentang V. TEOREMA:   Semua basis untuk suatu ruang vektor berdimensi terhingga mempunyai jumlah vektor yang sama   Suatu ruang vektor berdimensi terhingga V, yang dinyatakan dengan dim(V), didefinisikan sebagai jumlah vektor dalam suatu basis untuk V. Ruang vektor nol mempunyai dimensi nol. Contoh Menentukan basis dan dimensi ruang solusi dari SPL homogen penyelesaian Kita dapat menyatakan sistem ini dalam bentuk sebagai beri
Baca selengkapnya

LIMIT FUNGSI TAK HINGGA

-
Gambar
 Pengertian limit fungsi tak hingga           Pengertian limit fungsi di tak hingga adalah sebagai berikut :  a.  Jika nilai suatu fungsi f mendekati L untuk x yang terus membesar menuju ∞ maka kita katakan bahwa f mempunyai limit L untuk x mendekati ∞ dan ditulis L xf  )(lim x = ∞→  (dibaca  limit f untuk x mendekati ∞ sama dengan L).   b.  Jika nilai suatu fungsi f terus membesar untuk x  menuju ∞ maka kita katakan bahwa f mempunyai limit ∞ untuk x mendekati ∞ dan ditulis ∞= ∞→  )(lim x xf  (dibaca  limit f untuk x mendekati ∞ sama dengan ∞).   c.  Jika nilai suatu fungsi f terus mengecil untuk x  menuju ∞ maka kita katakan bahwa f mempunyai limit ∞ − untuk x mendekati ∞ dan ditulis ∞= ∞→ -  )(lim x xf  (dibaca  limit f untuk x mendekati ∞ sama dengan ∞ − ). Rumus Cepat menyelesaikan limit tak terhingga Rumus cepat mengerjakan limit tak terhingga yang pertama dapat digunakan untuk bentuk soal limit tak terhingga pada bentuk pecahan. Untuk memperoleh nila
Baca selengkapnya

KONTINUITAS

-
Gambar
kontinuitas       Kontinuitas adalah kesinambungan. Lawan dari kontinuitas adalah diskontinuitas yaitu tidak kesinambungan. Kontinuitas suatu fungsi kurang lebih sama artinya dengan kesinambungan suatu fungsi. f ( x ) f ( x ) kontinu di x = a x = a jika lim x → a + f ( x ) = lim x → a − f ( x ) = f ( a ) lim x → a + f ( x ) = lim x → a - f x = f ( a ) Keterangan : x → a + x → a + artinya x x mendekati a a dari kanan x → a − x → a - artinya x x mendekati a a dari kiri Tidak kontinu sama artinya dengan diskontinu Syarat kontinuitas suatu fungsi       fungsi f(x) dikatakan kontinu pada suatu titik x = a bila : Note :  a -  a + ,tanda + dan - hanya menunjukkan arah        contoh soal : 
Baca selengkapnya