DETERMINAN DENGAN METODE CHIO

Determinan Matriks

Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atau . Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.

Dalam bidang aljabar linear, determinanadalah nilai yang dapat dihitung dari unsur suatu matriks persegi. Determinan matriks Aditulis dengan tanda det(A), det A, atau |A|. Determinan dapat dianggap sebagai faktor penskalaan transformasi yang digambarkan oleh matriks.

Determinan MatriksOrdo 2 x 2

Sunting

Determinan adalah suatu fungsi tertentu yang menghubungkan suatu bilangan real dengan suatu matriks bujursangkar.

Sebagai contoh, kita ambil matriks A_2x2

A = ${\displaystyle {\begin{bmatrix}a&b\\c&d\\\end{bmatrix}}}$ tentukan determinan A

untuk mencari determinan matrik A maka,

det(A) = ad - bc

Contoh Soal:

A = ${\displaystyle {\begin{bmatrix}1&2\\4&5\\\end{bmatrix}}}$ tentukan determinan A

Jawab:

det(A) = ${\displaystyle {\begin{bmatrix}1&2\\4&5\\\end{bmatrix}}}$ = 1x5 - 4x2 = -3

Determinan Matriks Ordo 3 x 3

Determinan dengan Ekspansi KofaktorSunting

Terbagi tiga jenis yaitu:

• Dengan Minor dan Kofaktor
• Dengan Ekspansi Kofaktor Pada Baris Pertama
• Dengan Ekspansi Kofaktor Pada Kolom Pertama

Determinan dengan Minor dan kofaktorSunting

A = ${\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}}$ tentukan determinan A

Pertama buat minor dari a₁₁

M₁₁ = ${\displaystyle {\begin{bmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\\\end{bmatrix}}}$ = detM = a₂₂a₃₃ - a₂₃a₃₂

Kemudian kofaktor dari a₁₁ adalah

c₁₁ = (-1)¹⁺¹M₁₁ = (-1)¹⁺¹a₂₂a₃₃ - a₂₃a₃₂

kofaktor dan minor hanya berbeda tanda C_ij=±M_ij untuk membedakan apakah kofaktor pada _ij adalah + atau - maka kita bisa melihat matriks di bawah ini

${\displaystyle {\begin{bmatrix}+&-&+&-&+&\cdots \\-&+&-&+&-&\cdots \\+&-&+&-&+&\cdots \\-&+&-&+&-&\cdots \\\vdots &\vdots &\vdots &\vdots &\vdots &\\\end{bmatrix}}}$

Begitu juga dengan minor dari a₃₂

M₃₂ = ${\displaystyle {\begin{bmatrix}a_{11}&a_{13}\\a_{21}&a_{23}\\\end{bmatrix}}}$ = detM = a₁₁a₂₃ - a₁₃a₂₁

Maka kofaktor dari a₃₂ adalah

c₃₂ = (-1)³⁺²M₃₂ = (-1)³⁺² x a₁₁a₂₃ - a₁₃a₂₁

Secara keseluruhan, definisi determinan ordo 3x3 adalah

det(A) = a₁₁C₁₁+a₁₂C₁₂+a₁₃C₁₃

Contoh Soal:

A = ${\displaystyle {\begin{bmatrix}1&2&3\\4&5&4\\3&2&1\\\end{bmatrix}}}$ tentukan determinan A dengan metode Minor dan kofaktor

Jawab:

c₁₁ = (-1)¹⁺¹${\displaystyle {\begin{bmatrix}5&4\\2&1\\\end{bmatrix}}}$ = 1 (-3) = -3

c₁₂ = (-1)¹⁺²${\displaystyle {\begin{bmatrix}4&4\\3&1\\\end{bmatrix}}}$ = -1 (-8) = 8

c₁₃ = (-1)¹⁺³${\displaystyle {\begin{bmatrix}4&5\\3&2\\\end{bmatrix}}}$ = 1 (-7) = -7

det(A) = 1 (-3) + 2 (8) + 3 (-7) = -8

Determinan dengan Ekspansi Kofaktor Pada Baris PertamaSunting

Misalkan ada sebuah matriks A_3x3

A = ${\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}}$

maka determinan dari matriks tersebut dengan ekspansi kofaktor adalah,

det(A) = a₁₁${\displaystyle {\begin{bmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\\\end{bmatrix}}}$ - a₁₂${\displaystyle {\begin{bmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\\\end{bmatrix}}}$ + a₁₃${\displaystyle {\begin{bmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\\\end{bmatrix}}}$

= a₁₁(a₂₂a₃₃ - a₂₃a₃₂) - a₁₂(a₂₁a₃₃ - a₂₃a₃₁) + a₁₃(a₂₁a₃₂ - a₂₂a₃₁)

= a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂- a₁₃a₂₂a₃₁ - a₁₂a₂₁a₃₃ - a₁₁a₂₃a₃₂

Contoh Soal:

A = ${\displaystyle {\begin{bmatrix}1&2&3\\4&5&4\\3&2&1\\\end{bmatrix}}}$ tentukan determinan A dengan metode ekspansi kofaktor baris pertama

Jawab:

det(A) = ${\displaystyle {\begin{bmatrix}1&2&3\\4&5&4\\3&2&1\\\end{bmatrix}}}$ = 1${\displaystyle {\begin{bmatrix}5&4\\2&1\\\end{bmatrix}}}$ - 2${\displaystyle {\begin{bmatrix}4&4\\3&1\\\end{bmatrix}}}$ + 3${\displaystyle {\begin{bmatrix}4&5\\3&2\\\end{bmatrix}}}$ = 1(-3) - 2(-8) + 3(-7) = -8

Determinan dengan Ekspansi Kofaktor Pada Kolom PertamaSunting

Pada dasarnya ekspansi kolom hampir sama dengan ekspansi baris seperti di atas. Tetapi ada satu hal yang membedakan keduanya yaitu faktor pengali. Pada ekspansi baris, kita mengalikan minor dengan komponen baris pertama. Sedangkan dengan ekspansi pada kolom pertama, kita mengalikan minor dengan kompone kolom pertama.

Misalkan ada sebuah matriks A_3x3

A = ${\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}}$

maka determinan dari matriks tersebut dengan ekspansi kofaktor adalah,

det(A) = a₁₁${\displaystyle {\begin{bmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\\\end{bmatrix}}}$ - a₂₁${\displaystyle {\begin{bmatrix}a_{21}&a_{23}\\a_{31}&a_{33}\\\end{bmatrix}}}$ + a₃₁${\displaystyle {\begin{bmatrix}a_{21}&a_{22}\\a_{31}&a_{32}\\\end{bmatrix}}}$

= a₁₁(a₂₂a₃₃ - a₂₃a₃₂) - a₂₁(a₂₁a₃₃ - a₂₃a₃₁) + a₃₁(a₂₁a₃₂ - a₂₂a₃₁)

= a₁₁a₂₂a₃₃ + a₂₁a₂₃a₃₁ + a₃₁a₂₁a₃₂- a₂₂(a₃₁)² - (a₂₁)²a₃₃ - a₁₁a₂₃a₃₂

Contoh Soal:

A = ${\displaystyle {\begin{bmatrix}1&2&3\\4&5&4\\3&2&1\\\end{bmatrix}}}$ tentukan determinan A dengan metode ekspansi kofaktor kolom pertama

Jawab:

det(A) = ${\displaystyle {\begin{bmatrix}1&2&3\\4&5&4\\3&2&1\\\end{bmatrix}}}$ = 1${\displaystyle {\begin{bmatrix}5&4\\2&1\\\end{bmatrix}}}$ - 4${\displaystyle {\begin{bmatrix}2&3\\2&1\\\end{bmatrix}}}$ + 3${\displaystyle {\begin{bmatrix}2&3\\5&4\\\end{bmatrix}}}$ = 1(-3) - 4(-4) + 3(-7) = -8

Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.

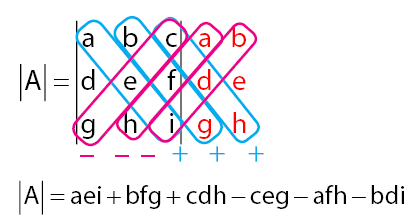
Contoh Soal:

A = ${\displaystyle {\begin{bmatrix}1&2&3\\4&5&4\\3&2&1\\\end{bmatrix}}}$ tentukan determinan A dengan metode sarrus

Jawab:

det(A) = ${\displaystyle {\begin{bmatrix}1&2&3&1&2\\4&5&4&4&5\\3&2&1&3&2\\\end{bmatrix}}}$ = (1x5x1 + 2x4x3 + 3x4x2) - (3x5x3 + 2x4x1 + 1x4x2) = 53 - 61 = -8