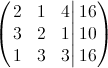Aljabar dan linear

DIAGONALISASI Masalah Diagonalisasi .  Diberikan sebuah operator linier T : V → V pada sebuah ruang vector berdimensi berhingga, apakah terdapat sebuah basis untuk V terhadap mana matriks T diagonal?      Jika A adalah matriks untuk  T : V→ V yang bertalian dengan beberapa basis sembarang, maka soal ini ekivalen dengan menanyakan apakah terdapat perubahan basis sehingga matriks baru untuk  T diagonal. Menurut teorema 8 dalam bagian 5.5, matriks baru untuk  T  akan sama dengan  P -1  AP  dimana  P  adalah matriks transisi yang sesuai. Jadi, kita sampai kepada perumusan matriks berikut yang berbentuk masalah diagonalisasi. Bentuk matriks dari masalah diagonalisasi .  Diketahui matriks kuadrat A, apakah terdapat matriks P yang dapat dibalik sehingga P -1  AP diagonal? Masalah ini menyarankan definisi – definisi berikut. Definisi.   Matriks kuadrat A dinamakan dapat  didiagonalisasi ( diagonalizable) jika terdapat matriks  P  yang dapat dibalik sehingga  P -1  AP  diagonal; ma

Eliminasi Gauss Metode eliminasi gauss termasuk dalam metode penyelesaian persamaan linear dengan cara langsung. Inti dari metode ini adalah membawa persamaan kedalam bentuk matriks dan menyederhanakan matriks menjadi bentuk segitiga atas. Setelah mendapat bentuk matriks tersebut dilakukan subtitusi balik untuk mendapat nilai dari akar persamaan tadi. Untuk lebih jelasnya kita perhatikan contoh berikut. Contoh eliminasi Gauss dan eliminasi Gauss-Jordan Selesaikan bentuk SPL berikut: 2x 1  + x 2  + 4x 3  = 16 3x 1  + 2x 2  + x 3  = 10 x 1  + 3x 2  + 3x 3  = 16 dalam bentuk matriks: Penyelesaian (Eliminasi Gauss): Langkah (1) Langkah (2) Langkah (3) Langkah (4) Langkah (5) Langkah (6)  langkah (7) Dengan demikian diperoleh: Untuk memperoleh x 1  dan x 2  subt pers (3) ke pers. (1) dan (2), x 3  = 3 x 2  – 10(3) = -28 x 2  – 30 = -28 x 2  = 2 Untuk memperoleh x 1: Jadi diperoleh x 1  = 1, x 2  = 2